Timer on Trees

You must already be familiar with the classic DFS algorithm

dfs(src, par):
    for(child : adj[src]):
        if(child != par):
            dfs(child, src)

The algorithm recursively traverses all the descendants of src before completing the DFS call for src. Let’s define 2 events, discovery and finish. When we visit an unvisited vertex for the first time, we say that the node was discovered. And once we have explored all its children, we mark it as finished.

Suppose we also track the time of each event. Let’s see how this extra information can help us solve a variety of problems.

dfs(src, par):
    tin[src] = ++timer
    for(child : adj[src]):
        if(child != par):
            dfs(child, src)

    tout[src] = ++timer

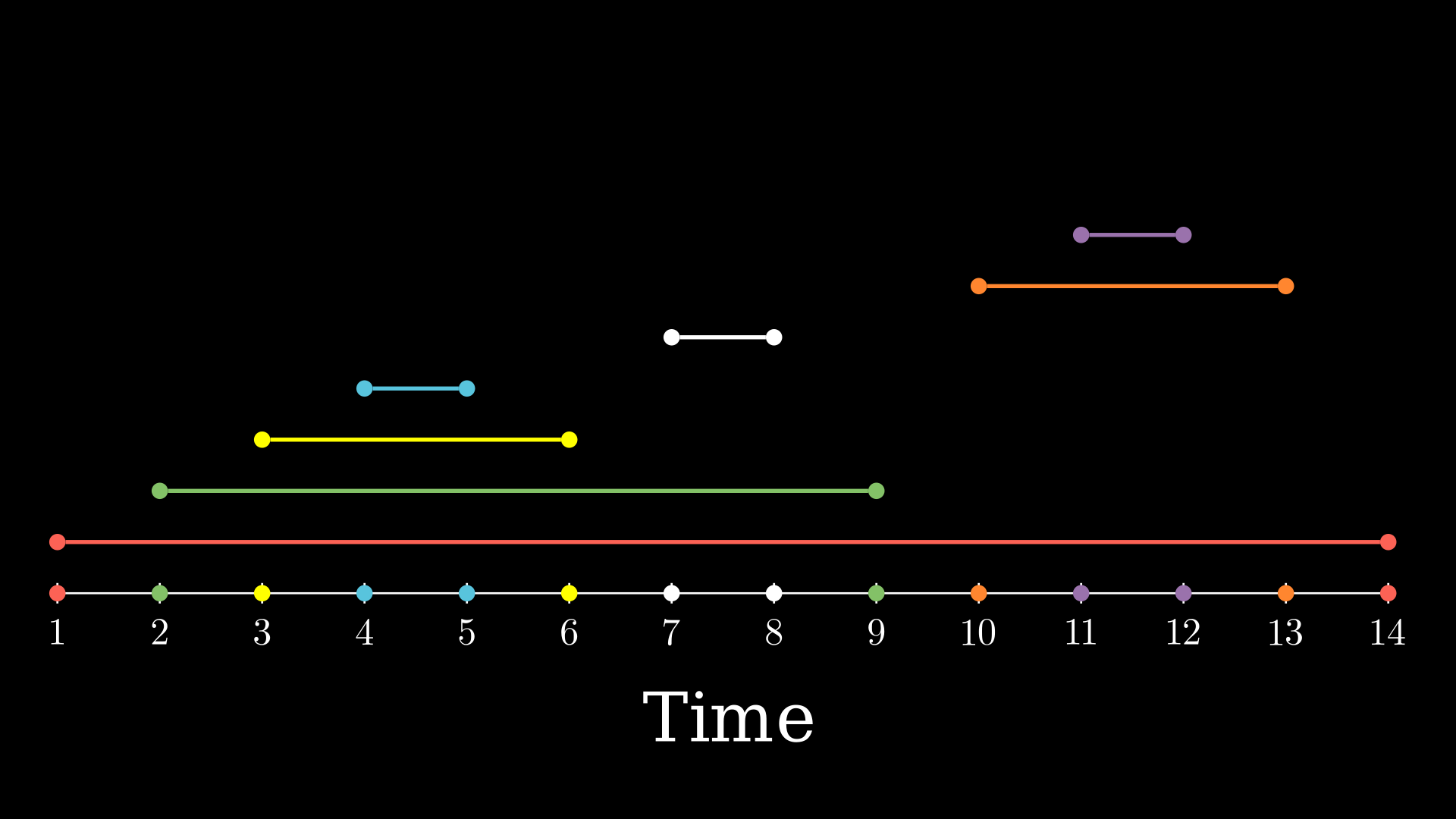
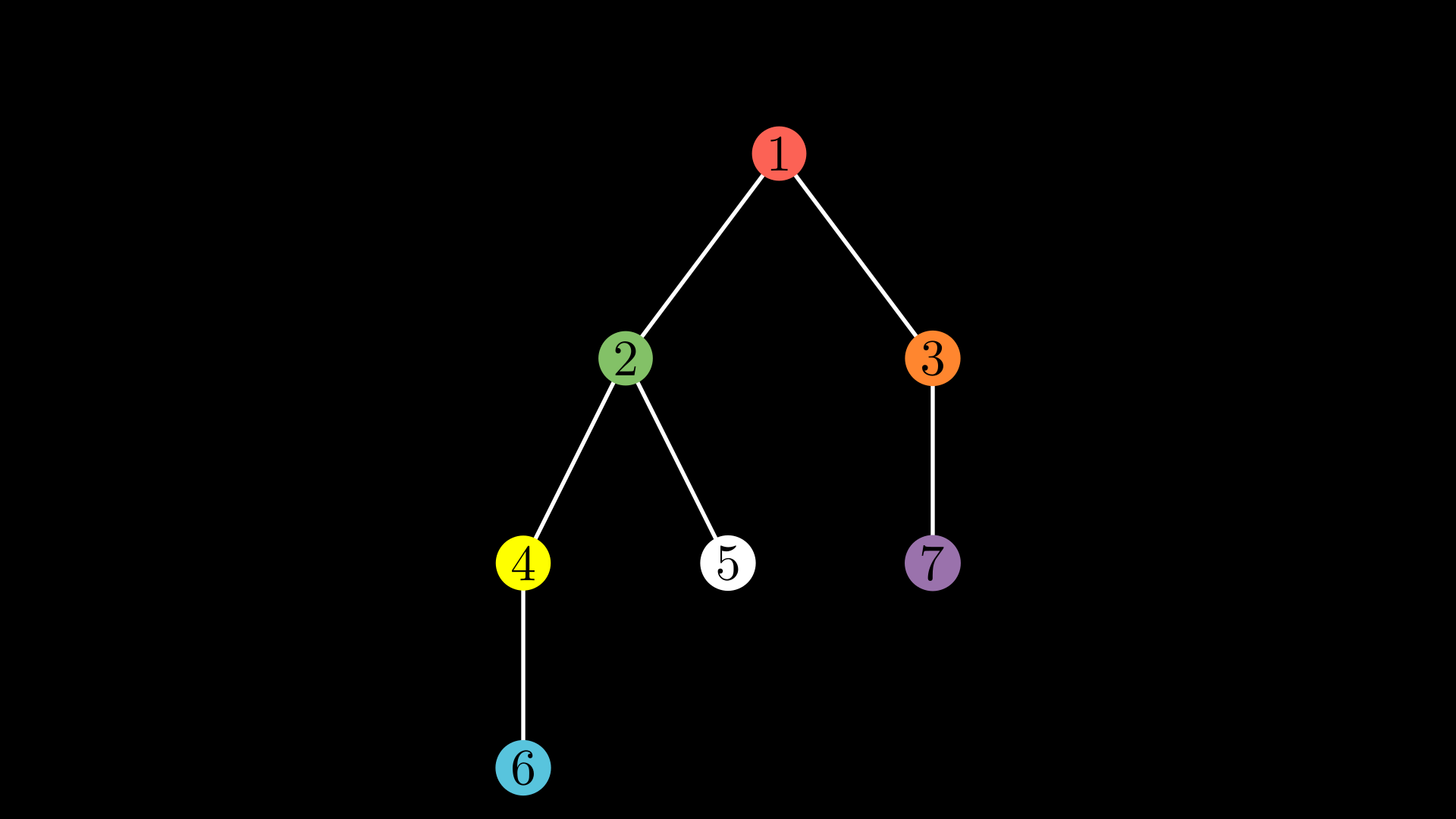
Given a tree, for any pair of vertices (u, v), exactly one of these always holds :

1. The interval (tin[u], tout[u]) and (tin[v], tout[v]) are disjoint and neither u nor v are ancestors of the other.
2. The interval (tin[u], tout[u]) is contained entirely within the interval (tin[v], tout[v]) and v is an ancestor of u.
3. The interval (tin[v], tout[v]) is contained entirely within the interval (tin[u], tout[u]) and u is an ancestor of v.

The following examples have a trivial solution using DP on Trees, but try to solve them using the concept of timer and event array only. This will help you build intuition on how operations on a tree can be transformed to operations on a subarray (which is easier to analyze).

Problem Link

Given vertices (u, v), determine which statement is true:

1. u is an ancestor of v
2. v is an ancestor of u
3. None of the above

This is a direct application of the Parenthesis theorem.

u is an ancestor of v iff tin[u] <= tout[v] and tout[u] >= tout[v].

You can find the code here

Problem Link

For each node, how to compute the number of nodes in its subtree?

Notice that, at each second, either a vertex is discovered for the first time, or it’s seen for the last time. Hence, if a clock ticks each time an event happens, there will be exactly 2*N events. Moreover, each point in the interval (tin[u], tout[u]) corresponds to an event that must have happend in the subtree of u. Since each node in its subtree triggers 2 events, we can deduce that there are as many nodes as the half length of that interval.

There will be a total of 2*N events, numbered from 1 to 2*N.

You can find the code here

Problem Link

For each node, print the sum of all values of nodes in its subtree.

Till now, we have only visualized the 2N events as points on the number line. Let’s get creative. Notice that each of the 2N points on the number line represent either a discovery or a finish event. Let’s create an array, event and everytime a vertex is discovered, we set event[tin[u]] = value[u]. Let’s keep the slots corresponding to finish time empty.

With this construction, you can notice that if you sum up all the non empty values of the subarray event[tin[u]...tout[u]], you’ll get the sum of all nodes in the subtree of u.

To optimize the time complexity, you can convert the event array to a prefix sum array to answer range sum queries in O(1).

When dealing with subtree queries, keep event[tin[u]] = value[u] and event[tout[u]] = {}.

The sum of subarray event[tin[u]...tout[u]] is the sum of subtree of u.

You can find the code here

Problem Link

For each node, compute the maximum sum of nodes encountered on any downward path.

Let’s create the event array again, but this time, instead of keeping empty slots for finish time, we set event[tout[u]] = - value[u].

Notice that each prefix sum of the subarray event[tin[u]...tout[u]] corresponds to a downward path starting from u. Hence, you can take the maximum of all prefix sums to get the best downward path.

When dealing with path queries, keep event[tin[u]] = value[u] and event[tout[u]] = - value[u]

Every prefix sum of the subarray event[tin[u]...tout[u]] is a downward path sum from u.

You can find the code here

Problem Link

Pick any node L and let’s compute the answer when L is the LCA of u and v. L can only be an LCA if u and v lie in different subtree of L. Every prefix starting from L denotes a downward path. Hence, we just need to find out a way to partition the subarray so that we can quickly identify whether nodes u and v belong to the same subtree or not.

To do this, we need to establisha a relation between an event and the entity/node that caused the event to happen. Then, as we move along a prefix, whenever we encounter a finish event, we can check whether the entity corresponds to a direct children of u.

This approach works in O(N^2 * Log(N)). But it’s good enough for now.

Make sure that you get AC on at least the first 6 testcases.

Maintain an entity array for a 2 way mapping b/w event and nodes. To check if it is a start or finish event, get the corresponding entity, check the in-time of the entity and compare it with the event’s time.

Using this trick, for any node, you can partition and identify its subtrees as disjoint subarrays.

You can find the code here

If the editorial has these keywords:

• Euler Tour
• Tree Flattening

it’s most likely referring to the techniques discussed in this blog.

The motivation for writing this blog was problem E: Happy Life in University that appeared in Good Bye 2023 round.

If this concept appears 2 more times in any Codeforces round, I’ll add a Part 2 of this blog discussing more applications of this technique. Remind me of both these events on this Codeforces Blog.