DP on spanning subgraphs of a tree
Find the number of ways to arrange $n$ distinct persons.
We all know the answer $n!$ from combinatorics. Let us arrive at the same answer using DP.
Define $dp[i]$ to be the number of ways to arrange the first $i$ persons. What happens when you introduce the $(i + 1)th$ person? If the first $i$ people are seated in a configuration, there are $(i + 1)$ slots (gaps) in which you can place this new person. Hence,
$$ dp[i + 1] = (i + 1) \cdot dp[i] $$
This idea of extending current states to create new ones is pretty common in DP problems (and is the crux of the algorithms that follow). You can also read this tutorial that applies the idea to binary strings : Extending Binary Strings with DP
A spanning subgraph contains all vertices from the parent graph and a subset of edges from the parent graph. Given a tree, count the number of spanning subgraphs that can be created.
There are $n - 1$ edges in a tree. Each edge can either be present or absent in the subgraph. Since all of these choices are independent, the total number of configurations is $2^{n - 1}$.
Given a tree, count the number of spanning subgraphs in which the root vertex has degree exactly equal to $d$.
Define $dp[i][d]$ to be the number of spanning subgraphs of the subtree rooted at vertex $i$ such that in all of these subgraphs, the $i^{th}$ vertex always has degree $d$.
In each of the spanning subgraph, the root vertex can have degrees ranging from $0$ to $n - 1$. All of these cases are disjoint, hence the total number of spanning subgraphs is $\sum dp[root][d]$ for all possible $d$. We should be able to verify if this sum is indeed $2^{n - 1}$.
Consider any node $u$. We can assume that all the DP value of its children are populated correctly, since they are populated recursively via DFS. We just need to figure out how to combine these values to get the DP value of node $u$. We will use the extension strategy discussed in the factorial problem.
Start out with an isolated vertex $u$ and keep on adding children one by one, essentially extending the tree. Moreover, instead of adding all the configurations of the children’s subtree at once, we’ll add them degree by degree.
Consider all configurations of the subtree of $u$ with $deg[u] = d$. What happens when you attach a child $c$ with $deg[c] = now$ ?
- In the new configuration, we can choose to delete the edge between $u$ and $c$. Hence, if there are $dp[u][d]$ ways to achieve the left config independently and $dp[c][now]$ ways to achieve the right config independently, there would be $$ dp[u][d] \cdot dp[c][now] $$
ways to merge those configurations into one.
How does the merged configuration look like? Since we deleted the edge leading to child $c$, the degree of $u$ or $c$ does not change. Hence, this new construction would contribute to the number of ways to make $deg[u] = d$ when the child $c$ is incorporated into the graph.
- Or we could keep the edge leading to child $c$. However, even in this case, the number of new configurations would be $$ dp[u][d] \cdot dp[c][now] $$
How does the merged configuration look like? In the new configuration, the degree of $u$ as well as $c$ would increase by 1. But, we don’t care about the degree of $c$, as the current goal is to pouplate $dp[u][*]$. Hence, this consruction would contribute to the number of ways to make $deg[u] = d + 1$ when the child $c$ is incorporated into the graph.
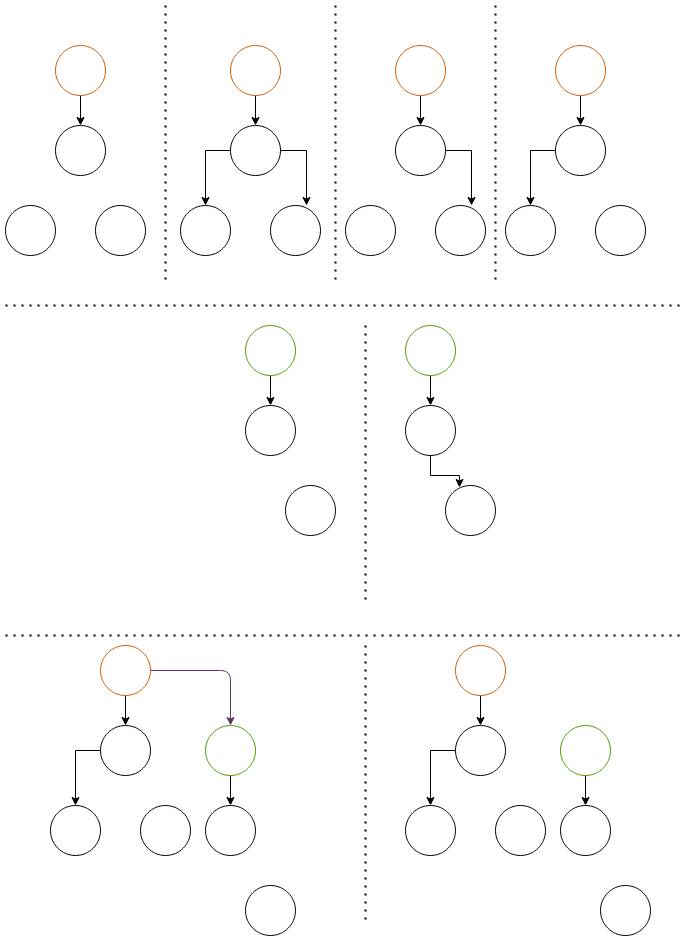
In the above image, you can see that we’ve already accumulated 2 children so far, and we want to investigate what happens when the third child is introduced. All of the 4 configuration on the top can be concatenated with 2 configuration from the bottom to create a new configuration. In this new configuration, if the we keep the purple edge (leading from orange to green cell), the degree of orange cell increases by 1. But if we decide to leave the purple edge, the degree remains the same.
When we try to introduce a child $c$ to the the subgraph, $dp[u][d]$ and $dp[u][d + 1]$ would be incremented by $dp[u][d] \cdot dp[c][now]$. However, doing these increments in-place is incorrect. This is because, a moment ago, $dp[u][d + 1]$ used to refer to the configuration in which the child was absent. Hence, if you mix the contribution with the child present, you would not be able to properly extend the graph rooted at $u$ with degree $d + 1$ since the original configuration value is lost.
Hence, we need an auxillary dp array, conveniently called $ndp$ (next dp) to temporarily store the number of configurations when the child $c$ is incorporated. Before we move on to the next child, we replace $dp[u][*]$ with $ndp[]$
This is another common technique in DP problems which avoids losing data of older states before ALL new states are computed correctly.
dfs(u, par):
dp[u][0] = 1
for c in adj[u]:
if c == par:
continue
dfs(c, u)
ndp = []
for d in range(adj[u].size):
for now in range(adj[c].size):
ndp[d] += dp[src][d] * dp[child][now];
ndp[d + 1] += dp[src][d] * dp[child][now];
swap(dp[u], ndp)
You can find the full code here
Given a tree, calculate the sum of $f$ over all spanning subgraph. $$ f(subgraph) = \prod deg(v)! $$
Original Problem which boils down to this subproblem
Warning: Reducing the problem to this subproblem is a difficult task. If you are not able to understand the editorial, skip it for now and just try to implement the reduced problem.
Define $dp[i][d]$ to be the sum of $f(subgraph)$ over all spanning subgraphs of the subtree rooted at vertex $i$ such that in all of these subgraphs, the $i^{th}$ vertex always has degree $d$.
How do we extend a subgraph by introducing a new child? Consider all configurations of the subtree of $u$ with $deg[u] = d$. What happens when you attach a child $c$ with $deg[c] = now$ ?
- In the new configuration, we can choose to delete the edge between $u$ and $c$. But now, for the new configuration, it is not at all clear how to recompute the new $f$ values. Blindly taking product like last time shouldn’t work (or would it?), because the $f$ value from the left and right configuration needs to be removed and a new $f$ needs to be added. All of this looks complex, because we don’t really store the individual $f$ of each configuration, we just store the sum of $f$.
But things would become simple, once you wonder what about what’s inside those summation terms. Suppose a total of 3 configurations are possible from the $u$’s subtree, and a total of 2 configurations are possible from the incoming child’s subtree. Then dp of the left half would contain summation of 3 terms $P_1 + P_2 + P_3$ where $P_i$ denotes the product obtained for a particular subgraph. Similary, the incoming child’s dp would contain summation of 2 terms $P_4 + P_5$.
Now, let us investigate what happens when we try to create new configurations.
From the the left half, we could choose the $P_1$ configuration and from the right half, we could choose either $P_4$ or $P_5$. Suppose we pick $P_4$. Then, in this new graph, the new value of $f$ would be $P_1 \cdot P_4$. This is because $f$ is defined as the degree-factorial product of ALL vertices. Hence, we should add $P_1 \cdot P_4$ to the new DP value. \[\begin{aligned} P_1 \cdot P_4 \\ P_1 \cdot P_5 \end{aligned}\]
We follow a similar strategy if we were to choose $P_2$ from the left half. \[\begin{aligned} P_2 \cdot P_4 \\ P_3 \cdot P_5 \end{aligned}\]
or if we were to choose $P_3$ from the left half. \[\begin{aligned} P_3 \cdot P_4 \\ P_3 \cdot P_5 \end{aligned}\]
Now, the new DP value would be sum of all these 6 values. So, let’s group them and sum them up. \[\begin{aligned} P_1 \cdot (P_4 + P_5) \\ P_2 \cdot (P_4 + P_5) \\ P_3 \cdot (P_4 + P_5) \end{aligned}\]
Once we take $(P_4 + P_5)$ common, we get this expression. This is nothing but $dp[u][d] \cdot dp[child][now]$ \[\begin{aligned} (P_1 + P_2 + P_3) \cdot (P_4 + P_5) \end{aligned}\]
Hence, the product strategy introduced in the counting problem works here as well.
How does the merged configuration look like? Since we deleted the edge leading to child $c$, the degree of $u$ or $c$ does not change. Hence, this new construction would contribute to the sum of $f$ such that $deg[u] = d$ when the child $c$ is incorporated into the graph.
- Or we could keep the edge leading to child $c$. This is where things get tricky.
From the the left half, we could choose the $P_1$ configuration and from the right half, we could choose either $P_4$ or $P_5$. Suppose we pick $P_4$. Of course, in the new graph, the $f$ value won’t be $P_1 \cdot P_2$ anymore, since the degree of both $u$ and $c$ has changed. Hence, we need to do a correction to the existing $f$ values. Let us figure out what terms are missing from the product. The degree of vertex $u$ is changing from $d$ to $d + 1$. Hence, if $deg(u)$ appears in the product, it should contribute $(d + 1)!$ But in previous configurations embeeded in $P_1$, it only contributions $d!$ How to do we ammend this? Simply multiply $P_1$ by $(d + 1)$, since $$ (d + 1)! = (d + 1) \cdot d! $$
Similary, the incoming child is going to retain the edge between $u$ and $c$. Hence, it should now contribute $(now + 1)!$ instead of the old $now!$ To ammend this, we can multiply $P_4$ by $(now + 1)$. \[\begin{aligned} (d + 1) \cdot P_1 \cdot P_4 \cdot (now + 1) \\ (d + 1) \cdot P_1 \cdot P_5 \cdot (now + 1) \end{aligned}\]
We repeat the same arguments for $P_2$. \[\begin{aligned} (d + 1) \cdot P_2 \cdot P_4 \cdot (now + 1) \\ (d + 1) \cdot P_2 \cdot P_5 \cdot (now + 1) \end{aligned}\]
We repeat the same arguments for $P_3$. \[\begin{aligned} (d + 1) \cdot P_3 \cdot P_4 \cdot (now + 1) \\ (d + 1) \cdot P_3 \cdot P_5 \cdot (now + 1) \end{aligned}\]
Combining them as before, we get \[\begin{aligned} (P_1 + P_2 + P_3) \cdot (P_4 + P_5) \cdot (d + 1) \cdot (now + 1) \end{aligned}\]
Hence, the product logic from before still works, but with some corrections. Of course, this new contribution should be provided to the configuration with degree of $u$ as $d + 1$.
dfs(u, par):
dp[u][0] = 1
for c in adj[u]:
if c == par:
continue
dfs(c, u)
ndp = []
for d in range(adj[u].size):
for now in range(adj[c].size):
ndp[d] += dp[src][d] * dp[child][now]
ndp[d + 1] += dp[src][d] * dp[child][now] * (d + 1) * (now + 1)
swap(dp[u], ndp)
You can find the full code here
The time complexity is $\mathcal{O}(n^2)$. But it’s not trivial to prove. For example, If $adj[u].size$ and $adj[c].size$ had been replaced by $n$, the time complexity would clearly be $\mathcal{O}(n^3)$ because we do $\mathcal{O}(n^2)$ operations in each node. However, we only iterate over the max possible degree of source and child, because we know that the other DP values are zero. And this makes all the difference.
Resources for the proof can be found here. I will add my own interpretation later.
The idea of extending a tree by adding children incrementally is very useful while solving Tree DP problems. Even though you might never come across problems asking you to compute sum of $f$ over subgraphs, you might still be able to use the main idea of extension and correction phase in other problems.
Given a tree, calculate the sum of $f$ over all spanning subgraph. $$ f(subgraph) = \sum deg(v) $$
If you’ve really understood the concepts discussed : DP on subgraphs, extension and correction phase, ndp, etc, try to implement this problem on your own. It is not straight-forward, but doable.
My initial plan was to add this problem as an example and add the factorial one as an exercise, since this was just sum over sum, how hard could it be as compared to sum over prod over factorial. But I was wrong. This one is more difficult. Can you guess the reason why? Let me know your answers on this Codeforces Blog. Or if you have an alternate easier approach, do let me know on the CF blog.
I will add my solution and explanation after some AC submissions.