Dijkstra in the streets, BFS in the sheets

Can you write/prove Dijkstra’s algorithm without referring to external sources? What about BFS? If your answer to the first question is NO, and to the second question is YES, this tutorial is for you.

The book Introduction to Algorithms has a section :

You can think of Dijkstra’s algorithm as generalizing breadth-first search to weighted graphs. A wave emanates from the source, and the first time that a wave arrives at a vertex, a new wave emanates from that vertex. Whereas breadth-first search operates as if each wave takes unit time to traverse an edge, in a weighted graph, the time for a wave to traverse an edge is given by the edge’s weight. Because a shortest path in a weighted graph might not have the fewest edges, a simple, first-in, first-out queue won’t suffice for choosing the next vertex from which to send out a wave.

In fact, this is the only thing that you need for all problems related to Dijkstra’s algorithm.

• Emanate a wave from vertex src.
• Repeat the following until no more waves are present:
  • Pick the visited vertex that the fastest wave arrived at.
  • Mark this vertex as visited.
  • Emanate new waves for all its children.

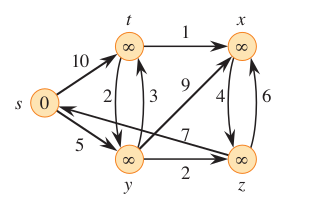
The wave starts at source. Hence, at time t = 0, the distance of src is 0, while all other distances are infinity.

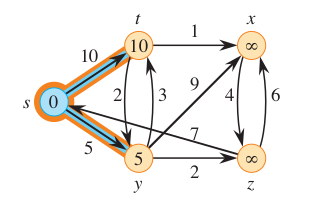
Now, two waves emanates from source 0. These waves will reach their target in 5 and 10 minutes respectively.

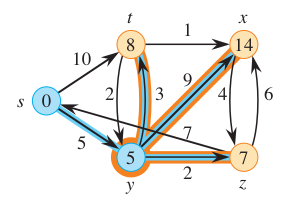
At time t = 5, the wave reaches vertex y. Three new waves would emerge from this vertex. The current time is 5 minutes, hence the wave towards vertex 8 will arrive at its target in 5 + 3 = 8 minutes. Hence, we can forget the other wave which is supposed to arrive at this vertex at time t = 10.

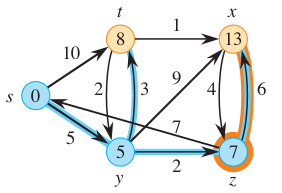
At time t = 7, the wave will reach vertex z. A new wave will emanate towards vertex x. Note that the previous traveling wave is supposed to reach vertex x at time t = 14 minutes. Hence, since this wave is faster (it reached in 13 minutes), we can ignore the older wave.

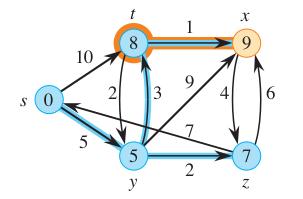
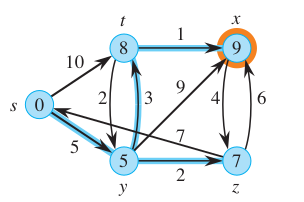
Time:

• t = 0 : A single wave reaches vertex s. s-t and s-y waves emanate from vertex s.
• t = 1 : Two waves are traveling towards y and t.
• t = 2 : Two waves are traveling towards y and t.
• t = 3 : Two waves are traveling towards y and t.
• t = 4 : Two waves are traveling towards y and t.
• t = 5 : The s-y wave reaches vertex y. Three new waves emanate, y-t, y-x and y-z.
• t = 6 : Four waves are traveling towards t, x and z.
• t = 7 : The y-z wave arrives at vertex z. A new wave z-x emanates.
• t = 8 : The y-t wave reaches vertex t. A new wave t-x emanates.
• t = 9 : The t-x wave reaches vertex x.
• t = 10 : The s-t wave arrives at vertex t. Since a faster wave already discovered this vertex, it is ignored.
• t = 11 : One wave is traveling towards x.
• t = 13 : One wave is traveling towards x.
• t = 14 : The y-x wave reaches vertex x. Since a faster wave already discovered this vertex, it is ignored.

Each time a wave reaches a vertex for the first time, the timestamp is the shortest distance of the node from src. As a consequence, we only need to run this algorithm n times.

If you’re still not convinced that Dijkstra is BFS behind the scenes, here’s a technique to convert the weighted graph to an equivalent unweighted graph. Pick any edge (u, v) with weight w. Now, delete this edge, and add w - 1 dummy vertices between u and v. Observe that a shortest path in the new graph corresponds to a shortest path in the original graph. Since the new graph is unweighted, you can use BFS to arrive at the answer. The dummy vertices also explain why the quote from CLRS talks about different speed of the waves, because the speed of the wave is directly proportional to the number of dummy vertices in between.

In problems that involve modifying the internals of Dijkstra, always think of unweighted graph first. If you can prove the correctness of your algorithm using BFS and dummy vertices, you are good to go.

Problem Link

The wave idea is already discussed above. For the dummy vertices, notice that if you add dummy vertices and perform BFS, the slower waves will arrive late to their destination because of large number of dummy vertices. Hence, BFS would correctly compute the shortest path.

You can find the code here. Focus on the O(n^2) code that has the concept of waves. The O(n log(n)) version just adds a fancy data structure to decrease the speed of the wave, and get the next wave that has reached its target.

You can now intuitively see why 0-1 BFS works. In this version, there are no dummy vertices, so normal BFS should work. Every time we process a node with level l, the level of child could be l or l + 1. Hence, if there are several nodes in level l, BFS should process them first before moving on to level l + 1. Morever, order of all nodes in the same level doesn’t matter. Hence, instead of using heaps, we could just utilize the front and back of a deque.

Given 2 vertices src and target, how to figure out if an edge lies on ANY shortest path from src to target?

Problem Link

You can submit your solution in the group contest. I will reveal the solution after a couple of AC submissions.

How to find the length of the second shortest path? Problem Link

Every minute, several waves propagate towards vertices. Then, once a wave reaches a vertex, it emits new waves. These new waves can overtake the older waves. Hence, the last overtake would be between the shortest and second shortest paths.

You can find the code here

You are given a graph containing white edges. There are additional black edges that originate from the source. Find out the maximal number of vertices whose shortest path can contain only white edges.

Let’s call a wave as infected if its ancestor contains atleast one black edge.

Every time a vertex emits new waves, it will overtake other waves if its speed is strictly greater than the slower wave. But if its speed is equal to the older wave, then an overtake would only happen if the current wave is not infected.

Hard version : Maximize the number of monochromatic shortest paths, and also print the minimum number of black edges needed.

Problem Link

While overtaking, if the speed of the waves are equal, and the older wave is not infected, there would be no overtake. But if it is infected, we should definitely overtake it. Why? Because we already paid the price of using the black edge in this wave, so it’s better to reuse it instead of paying the price for a new black edge again.

You can find the code here

When a wave emanates from a vertex, you look at the children and decide whether this is the fastest wave to reach a children or not. If it is the fastest wave, you update the timestamp for the children, else the children retain their estimated arrival time of the previous wave. This process is called Relaxing an edge.

If you need any hints for any of the problems, or if you have any queries about the intuition, you can ask on my discord server or twitter