Contribution Technique on Trees
Watch the video for a high level overview before reading the blog.
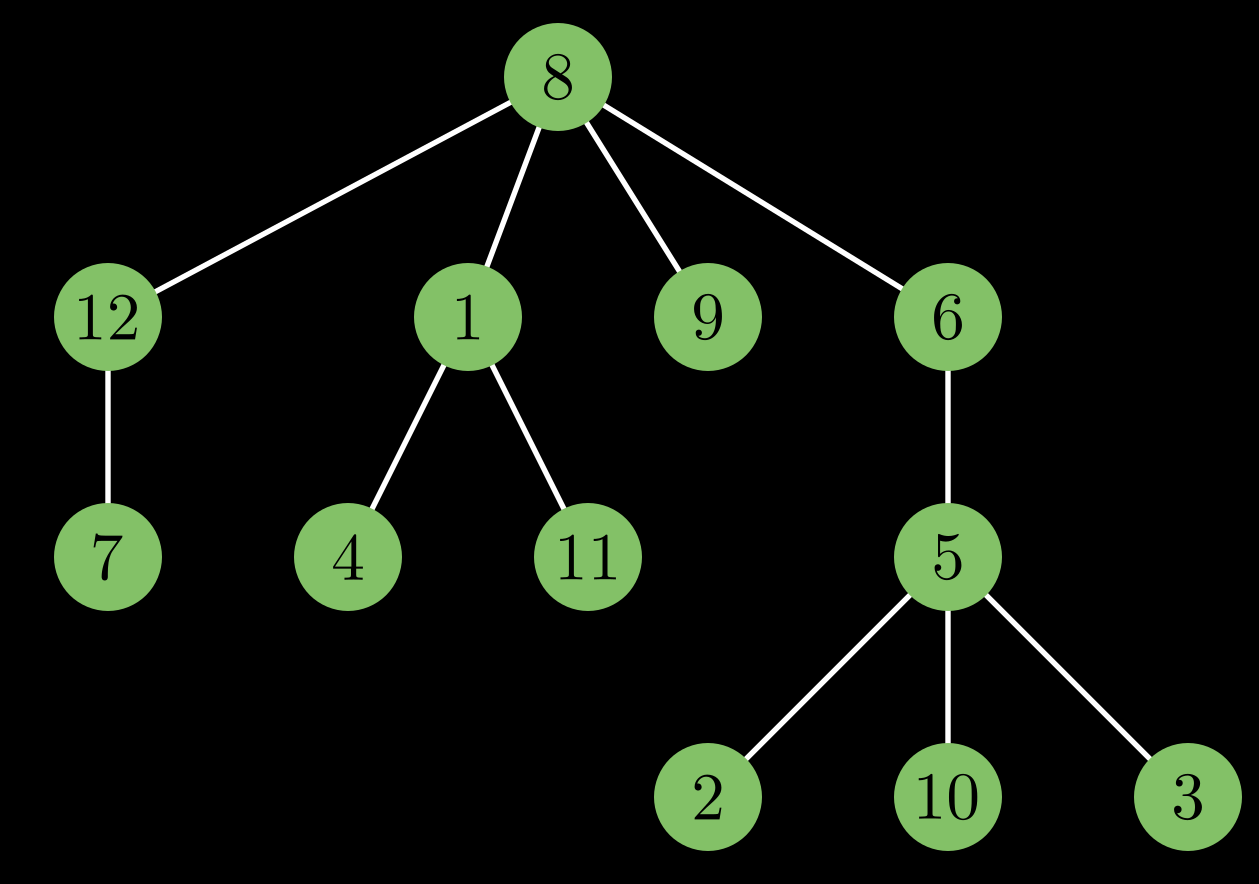You are given a rooted tree. How do you find out the distance between any 2 nodes?
Denote $d[u]$ to be the distance of node $u$ from the root. It can be calculated with simple Tree DP while doing a DFS on the tree. Then, $$dist(u, v) = d[u] + d[v] - 2 \cdot d[LCA(u, v)]$$ So, if you know how to compute the Lowest Common Ancestor of any 2 nodes, finding out the distance between any 2 nodes is easy.
But what if you don’t know how to compute LCA. Can you still solve this problem? It’s difficult. But what if I ask you to compute the distance between nodes $x$ and $x + 1$. But node $x$ and $x + 1$ can be located anywhere in the tree, so this problem is as difficult as the previous one.
But what if the tree had a special structure. Assume that the nodes of the tree are numbered in DFS order. In this special tree, can you find out the distance between node 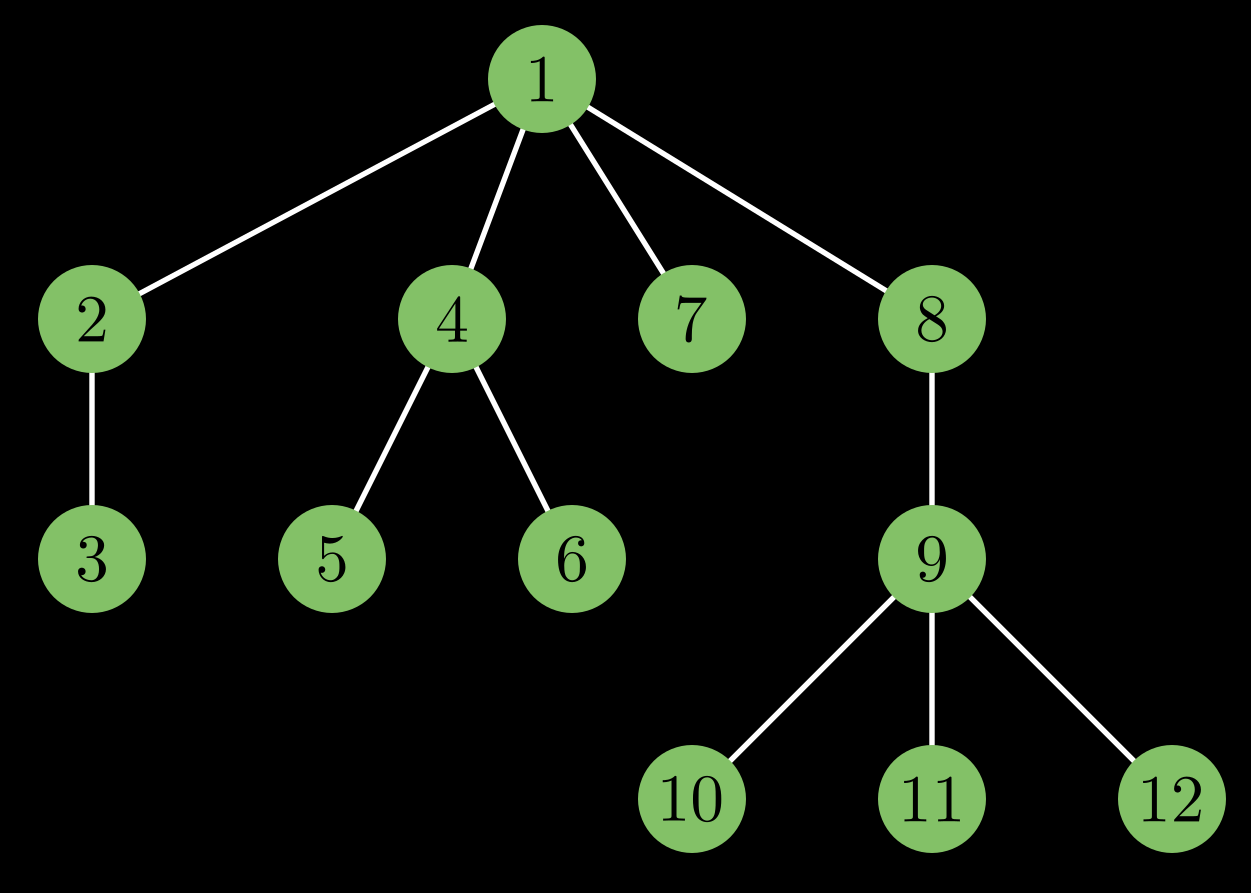$x$ and $x + 1$ without involving LCA?
What properties does this special tree have?
Consider the subtree of node $4$. Notice that all elements in its subtree are consecutive numbers greater than 4. Is this always true? Yes, a subtree of node $x$ will have all consecutive elements starting from $x + 1$.
The distance between node $x$ and $x + 1$ is usually one. But there are some nodes for which it is not one. For example $(3, 4)$, $(5, 6)$, $(6, 7)$, $(7, 8)$ $(10, 11)$, $(11, 12)$. What do these nodes have in common? They were the last leaf when you were doing the DFS on some subtree, hence it’s successor went into a different subtree.
But how do you identify the last leaf in the subtree? Note that the DFS order assigns label as soon as it encounters a node. Therefore, the last leaf in the subtree must have the highest label.
Define $mx[u]$ to the maximum label of a node in the subtree of node $u$. This can be computed with a simple Tree DP.
It is clear that the distance between $x$ and $x + 1$ is not 1 only if $x$ is equal to $mx[u]$ of some node $u$.
But, for each $x$, we can’t afford to check each $u$ and see if $mx[u] = x$. But can we do it the other way round? Let’s process each node $u$ and record somewhere that $mx[u]$ is one such vertex whose distance to its successor is not 1.
This is the first form of Contribution Technique where iterating one quantity over the other improved the time complexity from $O(n^2)$ to $O(n)$.
Now we know the list of nodes whose successor is somewhere far in another subtree. But is this information useful to us? Not really, because we still don’t know how far. Can we also figure out how far using Contribution Technique?
Let’s consider a path between 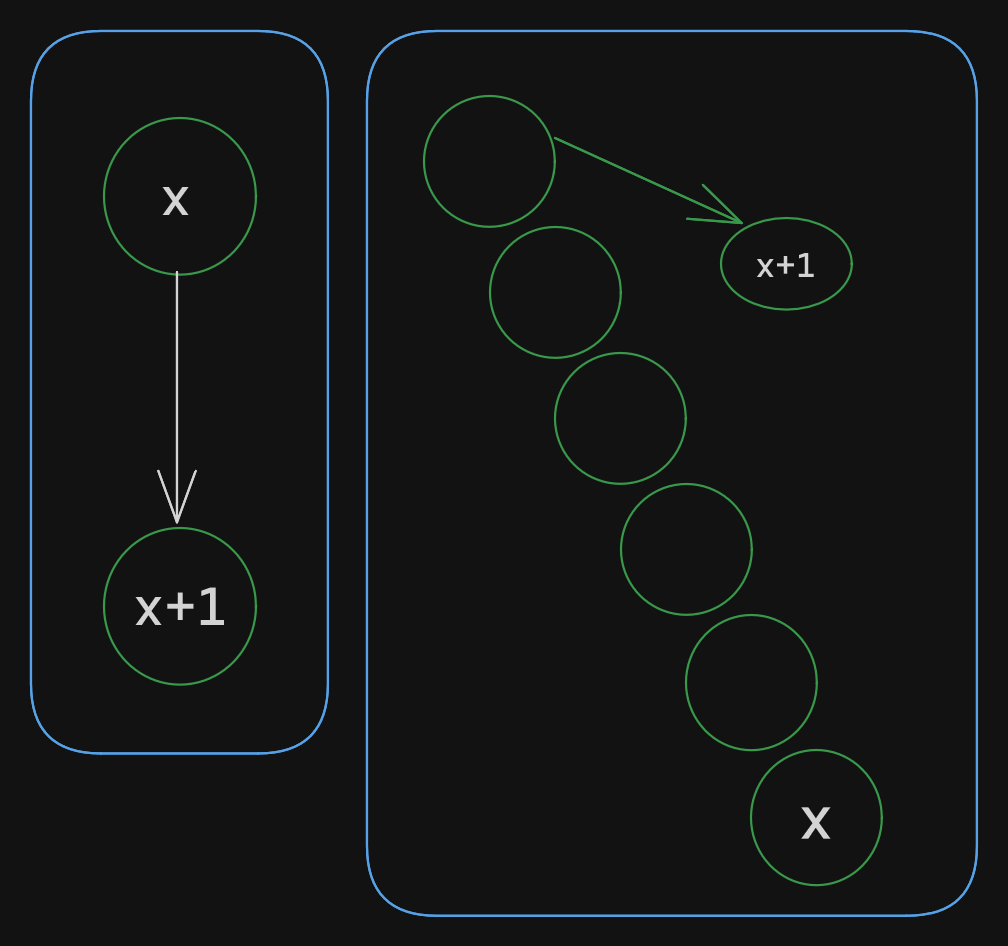$x$ and $x + 1$.
It is a combination of an upward path and a downward path. Notice that a downward path always has length 1.
This time, instead of processing nodes and marking $mx[u]$, let’s process edges and see what info we can extract.
Consider any edge $p \rightarrow c$. How many downward paths will it be a part of? Since a downward path has length 1, the journey has to end at node $c$. So, what are the starting points of the journey? There can only be one starting point, i.e. $c - 1$. But does this mean that $c - 1 = p$ if this edge acts as a downward path? No, because the path from $c - 1$ can originate from a different subtree, go upward and finally do down and end at $c$. But do we really care where $c - 1$ is located? No, because wherever it is, we’ve just found an edge that will be in its path. For example, look at the edge between $1 \rightarrow 7$ in the tree. Do we care about where 6 is? No. We just know that it HAS to cross this edge before reaching 7.
Therefore, each edge $p \rightarrow c$ will be a part of exactly one downward path, i.e, the one originating from $c - 1$.
Consider the edge $p \rightarrow c$ again. How many upward paths will it be a part of? Notice that when we were applying the contribution technique on the nodes, we said that only the vertex $mx[u]$ will have an upward path. Also, recall that an upward path descends down to a downward path of length 1 immediately if it finds the successor. So, the only upward paths that cross $p \rightarrow c$ are the ones which originated from the subtree of $c$ and hasn’t yet descended into a downward path. But every successor is already present in the subtree of $c$, so all paths must have already descended. Except one node, the last leaf, the vertex where the successor is not present in the subtree, hence it continues in the upward path. In the example above, the edge between $(1, 4)$ will be in the upward path starting from the maximum node in the subtree of $4$ which is $6$.
Therefore, each edge $p \rightarrow c$ will be a part of exactly one upward path, i.e, the one originating from $mx[c]$.
So, if we simply iterate over each edge, and increase the edge count for the originating node of the upward and downward path by 1, by the end of the process, for each node, we will have the total number of edges that it encounters on its path to the successor.
This is the second form of Contribution Technique. Notice how focusing on edges instead of nodes helped us to compute the answer faster.
void process_edge(int p, int c) {
int prev = (c - 1 + n) % n;
for (int v : {prev, mx[c]}) {
d[v]++;
}
}
void find_distances() {
for (int c = 1; c < n; c++) {
process_edge(parent[c], c);
}
for (int i = 0; i < n; i++) {
cout << d[i] << " ";
}
cout << "\n";
}
Let’s consider the weighted version of the DFS order tree. Assume each edge has a non-negative weight and none of the weights are revealed yet. But you do know that the total sum of weight on all edges is $total$.
For each edge, what will be the maximum distance possible between $x$ and $x + 1$, if you are allowed to assign any weight to unrevealed edges as long as total sum of weights is $total$? It has to be equal to $total$ since you can just assign this weight to any unrevealed edge on the path.
Now, what happens when I reveal some of the weights, such that $remain$ weights are not yet assigned. Notice that if all the edges between $x$ and $x + 1$ are revealed, then the distance is fixed. But if there is at least one unrevealed edge, then the maximum distance is equal to the sum of the weights of revealed edges on the path + $remain$.
Hence, we need a way to compute the number of free edges in each path, and the total sum of assigned edges in each path. Since every edge participates in exactly 1 upward and 1 downward path, it is easy to update this contribution.
void add_free_edge(int p, int c) {
int prev = (c - 1 + n) % n;
for (int v : {prev, mx[c]}) {
free_edges[v]++;
}
}
void remove_free_edge(int p, int c, long long w) {
int prev = (c - 1 + n) % n;
for (int v : {prev, mx[c]}) {
free_edges[v]--;
assigned[v] += w;
}
}
void reveal(long long remain) {
for (int c = 1; c < n; c++) {
add_free_edge(parent[c], c);
}
int cnt = n - 1;
while (cnt--) {
int x;
long long y;
cin >> x >> y;
x--;
remain -= y;
remove_free_edge(parent[x], x, y);
long long ans = 0;
for (int i = 0; i < n; i++) {
ans += assigned[i];
if (free_edges[i]) {
ans += remain;
}
}
cout << ans << " ";
}
cout << endl;
}
But what if the problem asked you to compute the sum of distance between successor?
In the Contribution Technique, our updates happen in $O(1)$, but we need to traverse the $free\_edges$ list every time to check how many paths have at least one edge. The time complexity is $O(n^2)$.
Can we optimize it somehow?
Yes, recall the trick that we use to do Topological Sorting via Kahn’s Algorithm. Instead of iterating over the vertices to figure out which new vertices have indegree 0, we rely on the fact that indegree is a decreasing function, so every time we delete a vertex from the graph, we immediately check if the neighbor’s indegree has become zero. If it has, we take it it in the queue, because its indegree can never increase.
We can use the same idea here. Notice that once a path has lost all the free edges, it will never be able to gain it back. So, we can keep 2 sets of vertices. The $free$ set contains all vertices whose path contains at least one free edge and a $locked$ set containing all vertices where all edges on the path are already determined. Notice that elements can only be transferred from $free$ set to $locked$ set.
Then, the answer is sum of the assigned edges of each path in the locked set + sum of assigned edges of each path in free set + remain*free_set_size
All of these quantities can be stored and updated in a variable. Once the last edge of a path is locked, you transfer the path from $free$ set to $locked$ set.
void add_free_edge(int p, int c) {
int prev = (c - 1 + n) % n;
for (int v : {prev, mx[c]}) {
free_edges[v]++;
}
}
void remove_free_edge(int p, int c, long long w) {
int prev = (c - 1 + n) % n;
for (int v : {prev, mx[c]}) {
free_edges[v]--;
assigned[v] += w;
unlocked_sum += w;
if (free_edges[v] == 0) {
unlocked_count--;
locked_sum += assigned[v];
unlocked_sum -= assigned[v];
}
}
}
void reveal(long long remain) {
for (int c = 1; c < n; c++) {
add_free_edge(parent[c], c);
}
unlocked_count = n, locked_sum = 0, unlocked_sum = 0;
int cnt = n - 1;
while (cnt--) {
int x;
long long y;
cin >> x >> y;
x--;
remain -= y;
remove_free_edge(parent[x], x, y);
long long ans = locked_sum + unlocked_sum + unlocked_count * remain;
cout << ans << " ";
}
cout << endl;
}
The last problem that we discussed is actually a 2000 Rated problem on Codefroces, which appeared as Problem E. Iris and the Tree in Codeforces Round 969. Even though the problem statement might look intimidating at first, with Contribution technique, the solution is pretty simple and elegant.
Make sure to upsolve the problem, first in $O(n^2)$ by manually maintaining the number of free edges for path of each vertex, and then optimizing it to $O(n)$ by maintaining variables for sum.