LIS using Trie

Consider the famous problem of finding the length of the Longest Increasing Subsequence of an array.

You might be familiar with the classical DP approach :

$dp[i]$ is the length of the LIS ending at index $i$.

The time complexity of this DP is $O(n^2)$ and it’s not possible to optimize this DP. But there’s another creative DP definition :

$dp[len]$ is the smallest element at which an increasing subsequence of length $len$ ends.

The time complexity of this DP is also $O(n^2)$, however using some observations, you can optimize it to $O(n\cdot log(n))$ with Binary Search.

There’s yet another DP definition, and this is by far the easiest one. :

$dp[val]$ is the length of the LIS ending at value $val$.

This DP is also $O(n^2)$ but you can optimize it to $O(n\cdot log(n))$ using Segment Tree.

These are the only possible ways I could find on the internet to solve LIS. In this tutorial, I will share a unique and novel approach to find the length of the LIS using a Trie, that can be implemented in just 10-15 lines of code.

Let’s start with this DP definition:

$dp[val]$ is the length of the LIS ending at value $val$.

If you append an element $x$, you can refresh the DP value of $x$ via

$dp[x]:=max(dp[s]:s<x)$

Hence, to optimize it, you need a data structure that can support prefix maximas while also supporting updates. You can definitely use a segment tree, but it’s possible to build such a data structure using a Binary Trie.

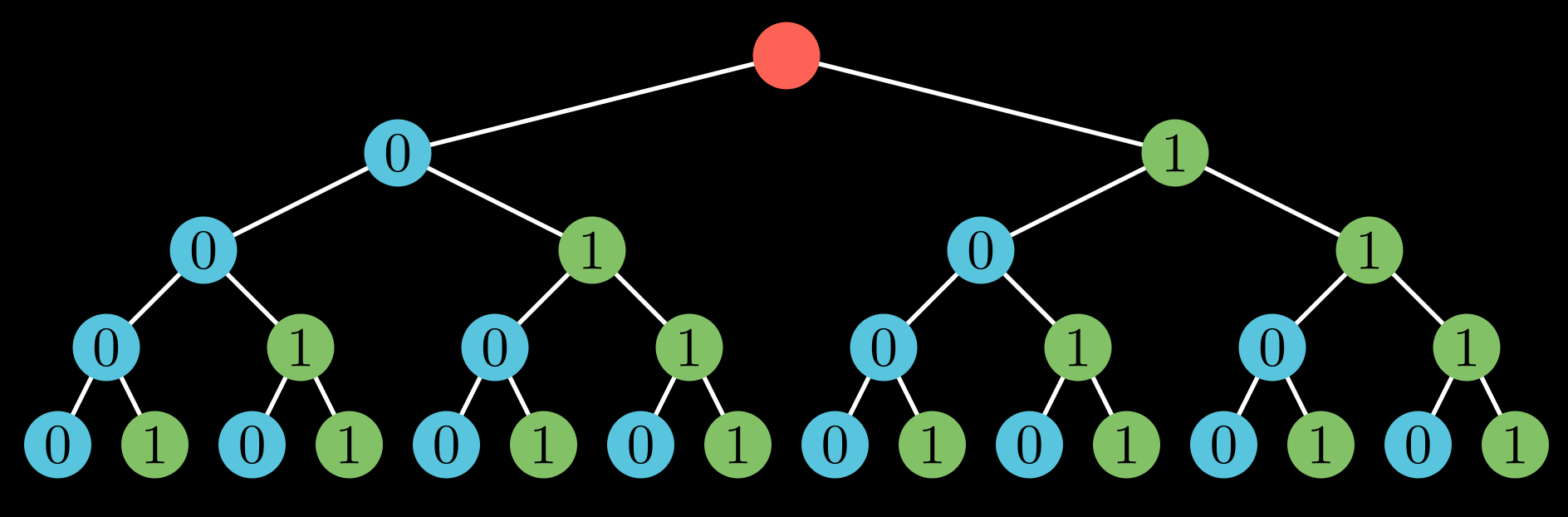Suppose all elements of the array can be represented via 4 bits. Consider a perfect binary tree on 4 levels where all levels are filled. Let’s color the left child in blue, and assign it a value of 0 and the right child in green and assign it a value of 1.

Then, notice that any number that can be represented using 4 bits can be found in this tree if you start from the root and traverse downwards. What’s more? Traversal of the leaves from left to right would result in a sorted sequence.

Let’s try to apply Tree DP. Each leaf stores $a[v]$ where $v$ is the value that this leaf represents. Then, define $dp[root]$ to be the maximum value of a leaf in the subtree of $root$. Then, $$dp[root]=max(dp[child])$$

Next, consider the binary representation of any number. What do numbers that are smaller than it look like?

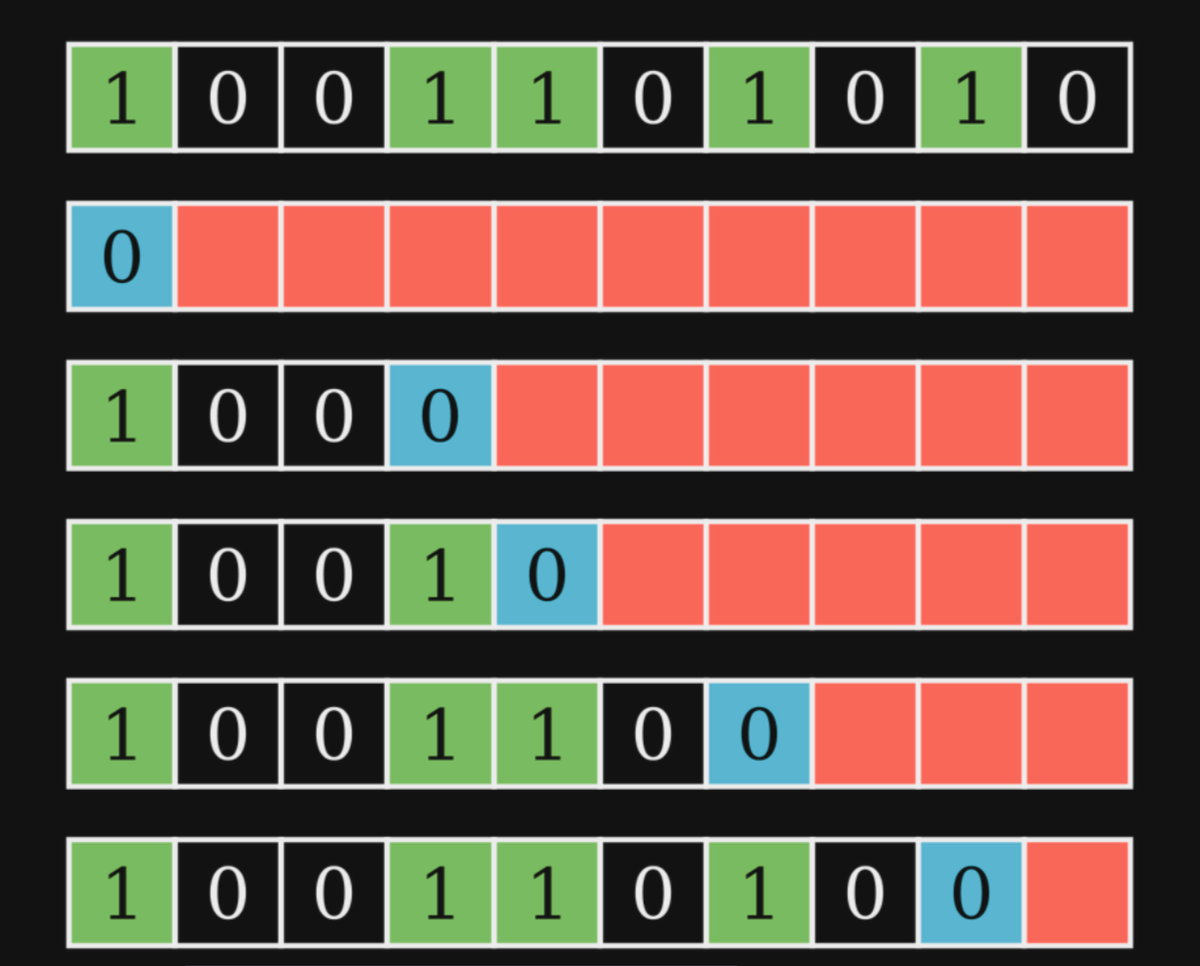
If $x<y$, then $x$ will have a common prefix with $y$, followed by a zero at the position where the bit is set in $y$, and the bits after that doesn’t matter. In the image above, the blue color represents the point of divergence, and the red color indicates bits that are irrelevant.

How do we traverse this tree to make sure we only visit smaller leaves? Notice the the point of divergence cannot be at an unset bit, therefore, as long as we encounter an unset bit in $y$, we should keep going to the left subtree. Now, the first time we encounter a set bit, we can either choose to keep it as a common prefix, in which case, we should move along the direction of $y$, or we can decide to diverge at this point. If you decide to make this as a point of divergence, you will move into the left subtree. But notice that all leaves in the left subtree are now strictly less than $y$. Therefore, we don’t actually need to go to the leaves to compute the maximum. We can use our precomputed value from Tree DP.

But while implementing the idea, we don’t actually need to create a perfect binary tree. If there at most ${10}^5$ numbers in the input, there can’t be $2^{30}$ leaves. Therefore, we can simply create each subtree on demand. This is a pretty standard idea that is used in Trie based problems, so I will skip it.

int query(int x) {
    int p = 1, ans = 0;
    for (int i = lg - 1; i >= 0; i--) {
        int bit = get_bit(x, i);
        if (bit) {
            int lchild = child[p][0];
            ans = max(ans, dp[lchild]);
        }
        p = child[p][bit];
    }
    return ans;
}

Congrats, you just created a data structure that can answer prefix maximas in $O(log(n))$. But how do you make it dynamic to support updates?

Once you update a leaf, notice that the only DP values that can possibly change are the ones on the path from root to this leaf. Since the height of the tree is $O(log(n))$, we can recompute the DP value of all nodes on this path recursively.

But for the LIS problem, the updates are very specific. Notice that the value at a leaf can only increase or remain the same. Therefore, we don’t even need to walk up the tree to recompute the DP value. We can simply do it on our downward path while locating the leaf.

void insert(int x, int val) {
    int p = 1;
    for (int i = lg - 1; i >= 0; i--) {
        int bit = get_bit(x, i);
        if (!child[p][bit]) {
            child[p][bit] = ++sz;
        }

        p = child[p][bit];
        dp[p] = max(dp[p], val);
    }
}

And that is it, we have a data structure that can support prefix maximas and point updates in $O(log(n))$. To solve the LIS problem, you can simply use the data structure like so

void solve(vector<int> &a) {
    int n = a.size();

    int ans = 0;
    for (int i = 0; i < n; i++) {
        int dp_val = 1 + query(a[i]);
        insert(a[i], dp_val);
        ans = max(ans, dp_val);
    }

    cout << ans << "\n";
}

You can submit your code on CSES : LIS

• Code for LIS on CSES